Walton P. Coutinho
- Post graduate research student
- Position
- Postgraduate Research Student
- Institution
- Mathematics (FSHS)
- Webpage
- http://www.southampton.ac.uk/maths/postgraduate/research_students/wpc1e14.page
- w.p.coutinho@soton.ac.uk
- walton.coutinho@gmail.com
- Contact
- Complete this online contact form to contact Walton.
My main research interests are in nonlinear and combinatorial optimisation. I am currently working on the development of algorithms for vehicle routing problems under motion constraints with applications to UAVs (i.e., drones, gliders). Problems like this are very challenging because they usually combine routing and trajectory optimisation, which are very challenging problems on their own. My current research is concerned about the Glider Routing and Trajectory Optimisation Problem (GRTOP) with applications to disaster assessment and response. In my previous research, I worked on the development of path planning algorithms for rotary wing drones and on the development of exact algorithms for the Close-enough Travelling Salesman Problem.
Gallery
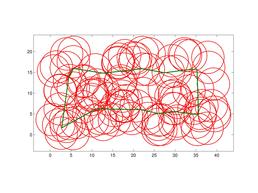
This is an optimal solution for Close-Enough Traveling Salesman Problem (CETSP) over an instance with 1000 vertices. In the CETSP, rather than visiting the vertex (customer) itself, the salesman must visit a specific region containing such vertex. To solve this problem, we proposed a simple yet effective exact algorithm, based on Branch-and-Bound and Second-Order Cone Programming (SOCP).
This is another CETSP solution for an instance with 100 vertices in a two-dimensional space.
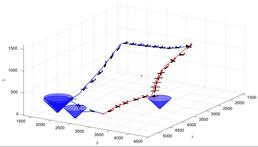
The Glider Routing and Trajectory Optimisation Problem (GRTOP) is the problem of finding simultaneously optimal routes and trajectories for a fleet of gliders with the aim of surveying a set of locations. We propose a novel Mixed-Integer Nonlinear Programming (MINLP) formulation for the GRTOP, which simultaneously optimises the routes as well as the flight path along these routes, while flight dynamics are modelled as constraints. We avoid solving a non-convex problem by linearising the gliders' flight dynamics, converting the proposed MINLP into a Mixed-Integer Second-order Cone Programming (MISOCP) problem. To allow for a more tractable formulation, the dynamical constraints are relaxed and a penalisation is added to the objective function. Several different discretisation techniques and solvers are compared. The formulation is tested on instances inspired by risk maps of flooding-prone cities across the UK and on 180 randomly generated instances.
This is an optimal solution for the GRTOP with 4 waypoints and 2 possible landing sites.