Patrick Bechlars

Position: Postgraduate Research Student
Institution: Engineering Sciences (FEE)
Webpage: http://www.bechlars.org/
Contact: Complete this online contact form to contact Patrick.

I completed my undergraduate studies in applied mathematics at the Karlsruhe Institute of Technology (KIT). Minor subjects included in this degree programme are mechanical engineering and computational sciences. Focus in the minor subjects was on Fluid Mechanics, High Performance Computing and Software Engineering. For my final thesis I developed characteristic boundary and interface conditions for numerical simulations of the Reynolds averaged Navier-Stokes equations.

In May 2011 I joined the Aerodynamics and Flight Mechanics (AFM) group as a research student. Under supervision of Richard D. Sandberg my work is concerned with the universality arguments for turbulence across different flow topologies. My study is part of the project `Is fine-scale turbulence universal?' in which I cover the part of direct numerical simulation (DNS) of a variety of compressible, turbulent flows including their post-processing and analysis.

Working with...

Richard Sandberg
Professor, Engineering Sciences (FEE)

Projects

Is fine-scale turbulence universal?

With Richard Sandberg (Investigator)

Gallery

Rotational structures of a turbulent jet shown as isosurfaces of the Q-criterion. This jet is created by a turbulent pipe flow exiting in a co-flow.

The supersonic, turbulent wake flow of an axisymetric cylinder is visulized by its mean flow (top) and an instantaneous snapshot (bottom) of rotational structures.

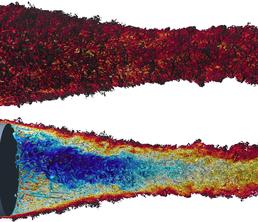
The supersonic, turbulent wake flow of an axisymetric cylinder is visulized by an instantaneous snapshot of rotational structures. The full wake is shown at the top and a longitudinal cut of the wake to reveal the structures in the recirculation region is shown at the bottom.

A turbulent flow inside a pipe is shown by visualizing rotational structures. A cross section of the pipe is shown on the left and a longitudinal cut is shown on the right. The coloured areas on the right highlight measurement sections.

The characteristical distribution of turbulent structures is shown by joint probability density functions of two invariants (Q,R) of the velocity gradient tensor at different wall-normal locations in the pipe. Wall distance is increasing from left to right.