Desiging Near-Capacity Quantum Error Correction Codes
- Started
- 2nd April 2012
- Research Team
- Zunaira Babar
- Investigators
- Lajos Hanzo
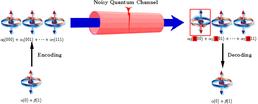
Application of quantum error correction codes:(1) Intended information qubit is encoded; (2) Transmission over a noisy quantum channel, which corrupts the first qubit. (3) Decoding successfully restores the qubit to its original state.
Quantum information processing provides an ultimate solution to our quest for miniaturization and higher processing power, revolutionizing the way we compute and communicate. Its inherent feature of quantum parallelism allows an exponential capacity and processing speedup, while quantum entanglement guarantees unconditional security. Unfortunately, these theoretical concepts cannot be readily implemented in real systems due to the presence of noise, which corrupts/disturbs the states of the quantum entities, `qubits'. This can be overcome by adding redundancy to the intended information, which helps in correcting the received information. However, the lack of near-capacity quantum error correction codes to counteract the noise experienced in real systems impedes the practical implementation of quantum computing and communication devices. By contrast, the corresponding classic systems are known to approach the capacity limits.
Against this backdrop, we aim to exploit the well-established classic code designs to derive near-capacity quantum codes. We will evaluate the performance of our systems by comparing their bit error ratio to that of the existing quantum codes as well as to the achievable capacity. We intend to base our comparisons on various channel models and conditions. These objectives will be achieved by conducting Monte Carlo simulations for the system. However, these simulations entail a high computational complexity as compared to the corresponding classic code designs. This is because an n-bit classic information sequence requires only an n-bit register, since it can only assume one of the 2^n values. By contrast, an n-qubit quantum information will require 2^n classic registers to save its value. Thus, the memory and processing requirements of these simulations increase exponentially. We can overcome this limitation by running our simulations on multiple computer processors on Iridis and averaging the results; thus, tasks, which would otherwise take weeks, can be accomplished in a few days.
Categories
Algorithms and computational methods: Distributed computing, Monte Carlo, Multi-core, Quantum Computation