Self Organized Network Routing using Quantum Evolutionary Methods

Started: 7th January 2013
Research Team: Dimitrios Alanis
Investigators: Lajos Hanzo

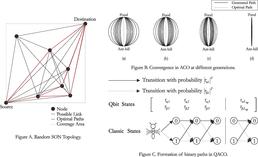
FIGURE. Random SON Topology (A), convergence in ACO at different generations (B), and formation of binary paths in QACO (C).

Self Organized Networks (SON) are, in general, fully interconnected wireless networking infrastructures with ad hoc architecture. The position of each node is not predetermined and, thus, their random deployment is enabled. In the simplest case, a message is forwarded from a source node into intermediate nodes so as to reach a destination node. As the nodes might be mobile and, therefore, have access to a restricted amount of energy, the path chosen should be optimal in terms of energy consumption. Moreover, some Quality of Service (QoS) requirements, such as for example, end-to-end delay and packet error rate, should be satisfied depending on the application. Hence, the optimization problem becomes a multi-objective one. In fact, the process of forming the optimal paths belongs to the family of the Travelling Salesman Problems (TSP), which has been found to be NP-hard as the number of possible destinations is increased. Therefore, the employment of suboptimal methods is essential in order to obtain the optimal solutions in polynomial time.

As mentioned in the abstract, the optimization methods employed were the Ant Colony Optimization (ACO) and its quantum inspired counterpart, the Quantum Ant Colony Optimization (QACO), which belong to the family of bio-inspired evolutionary algorithms. They are based on the fact that ants use chemical substances, often referred as pheromones, in order to communicate and locate their food. As each ant moves towards collecting its food from its nest it emits these substances for the rest ants of the colony to follow. Since they are considered to have poor eyesight, they would follow paths with increased pheromone intensity. In general, in each generation a constant number of ants are released and follow certain paths depending on their pheromone intensities; this procedure is repeated until convergence is achieved and the least rank Pareto front is exported. The main difference between these two methods is the fact that in the first the pheromones of the transitions from a node to another are represented by an (N-1) by (N-1) matrix, where N is the total number of nodes, while in the latter a quantum register representation is utilized. The parallel computing power of Iridis 3 was used in order to calculate in parallel using OpenMPI the solution vectors for the generated paths at each iteration. As for the objective function metrics, power consumption and packet error rate have been taken into account.

Computational Modelling Group

Self Organized Network Routing using Quantum Evolutionary Methods

Categories