Homogenisation of liquid crystal colloids

Started: 1st April 2013
Research Team: Thomas Bennett
Investigators: Giampaolo D'Alessandro, Keith Daly

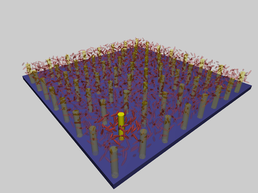
Visualisation of two dimensional geometry. Nematic liquid crystal (ellipsoids) containing an inclusion of pillars.

Nematic liquid crystals are composed of elongated rod like molecules. This phase of matter is characterized by long range orientational order; molecules tend to align their major axis. This orientational order leads to anisotropic material properties and a tendency to align in response to externally applied electric or magnetic fields. Nematics are studied for their technological application as well as for scientific interest due to their unique blend of solid and liquid properties.

Liquid crystals find a wide array of applications and are crucial elements of many optical devices. Suitability for applications is determined by the nematics material properties. For instance a material with lower elastic constants is more easily aligned by an applied field yielding a device with lower power requirements. An ongoing area of research involve studying doped nematics, dopants include metallic or dielectric nano particles of varying shapes and sizes. Dopants distort the ordering of the nematic host and lead to a change in effective material properties.

Suspensions of nano particles in liquid crystals have been studied by means of molecular simulations and macroscopic models. Simulations of rod like molecules are computationally expensive and are limited to small systems. On the other hand macroscopic models contain unknown phenomenological parameters that attempt to capture the coupling between liquid crystal and its dopant's. Unfortunately there is often no way to self consistently compute the value of these parameters. The aim of this project is to obtain a macroscopic description of a doped Nematic system that allows a consistent computation of the new dopant dependent terms.

We consider a uniform array (in two or three dimensions) of ellipsoidal particles inside a nematic host. On the surface of the ellipsoids the nematic obeys weak anchoring condition with a preferred alignment direction orthogonal to the dopant surface. We include the effect of an electric field on the alignment of the Nematic. We use mathematical homogenisation to transform the original system, consisting of the governing equations solved inside a detailed geometry, into a system of macroscopic equations inside a simpler geometry.

The outcome of the homogenisation process is that all of the complicated geometric information encoded in the original problem has been moved into effective material parameters. This is the crucial advantage over more phenomenological models. The microscopic detail is retained in the form of a cell problem, which is used to compute the effective material parameters. The end results of the process is twofold (i) we obtain equations that are less computationally intensive to solve and (ii) we can compute the new material parameters from the underlying geometry of the system.

In order to validate the method both the original system and the homogenised equations must be solved numerically. We use COMSOL run on Iridis4 to solve the governing equations in the complicated microscopic geometry. The homogenised equations are solved in MATLAB using a spectral collocation method.

Computational Modelling Group

Homogenisation of liquid crystal colloids

Categories