Using computer intensive methods to produce small area estimates of poverty
- Started
- 1st February 2011
- Ended
- 31st January 2014
- Research Team
- Steve Donbavand
- Investigators
- Nikolaos Tzavidis
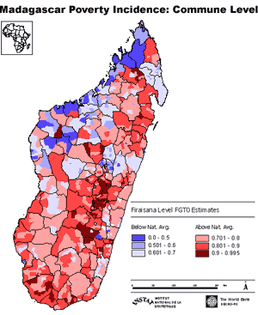
A poverty map of Madagascar produced by The World Bank which uses the most popular methodology. Amongst other findings, my work demonstrates that this method makes assumptions about the population which, if not fulfilled, can produce inefficient estimates
From social exclusion in the UK to the extreme destitution seen in sub-Saharan Africa, poverty reduction remains a key goal of policy makers around the world. Yet at the same time there is frustration that aid and development initiatives fail to reach those most in the need. The first step in designing well targeted programmes is a clear understanding of the geographical distribution of poverty throughout a country. This is known as a Poverty Map. Whilst this may sound like a simple concept, the highly localised nature of poverty means that useful Poverty Maps must be able to represent poverty at very low geographic levels. A region which appears relatively affluent may contain both poor areas and wealthy areas; it is critical that the poverty map highlights this. Estimates are typically based on income or consumption data collected through surveys. Unfortunately, by the time this data is disaggregated into usefully small geographic areas, the sample size tends to be too small to make reliable direct estimates. This therefore becomes a statistical problem of how to produce reliable estimates of poverty when sample size is small (known as Small Area Estimation). As the poverty measures are estimates, it is important to also provide an indication of the associated error through Mean Squared Error (MSE) estimates. Various methods of estimating poverty measures in small areas, and the associated MSE, have been proposed. My work begins with an empirical comparison of three of these methods and then goes on to suggest some modifications.
This work presents particular computational challenges. Because the poverty measures are non-linear functions of an underlying continuous variable (such as income), an analytical estimate would require the evaluation of high dimensional integrals. This is prohibitively complex, so an empirical approximation is used which requires Monte Carlo simulation of a large number of vectors. The same is true for the MSE estimation, where analytic estimation of the variance of complex parameters is not feasible and so a bootstrap procedure is used to obtain estimates of uncertainty. A single set of poverty estimates with corresponding MSE estimates therefore requires several hundred Monte Carlo cycles with each one containing several hundred bootstrap cycles. In order to achieve credible results, the methods, which are already computationally intensive, must then be applied many times to unique simulated populations. This therefore adds another cyclical layer on top of the Monte Carlo and bootstrap loops mentioned previously. The work would not have been practical on my desktop PC, but I was able to achieve some excellent result by splitting my jobs into batches and running them simultaneously on IRIDIS.
This research can help practitioners to make more accurate poverty estimates and in turn allow governments and other bodies to design targeted policies to alleviate poverty for those most in need.
Categories
Socio-technological System simulation: Human population
Algorithms and computational methods: Monte Carlo
Computational platforms: Iridis