Introducting Defects into the Ising Model

Started: 1st September 2012
Ended: 26th November 2012
Research Team: Benjamin Lowe

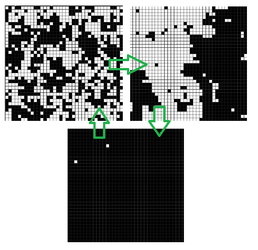
Graphical representation of the Ising model - showing phase changes.

The well-known Ising model, a model of emergent critical phenomenon and phase transitions, was reimplemented and extended to incorporate the study of defects in the lattice.

The Ising model, initially a statistical mechanics model of ferromagnetism formulated in 1924, has subsequently found a wide range of applications in many disciplines of Science. It is now a surprisingly versatile model of critical phenomena and phase transitions, particularly within statistical physics. A previously reported 2D Ising model was reimplemented and extended. In agreement with previous work, the model gave a critical temperature of 2.28±0.02, indicating that the reimplentation of the model was as expected. The model was further adapted in order to study the effects of randomly distributed 'defects'. These were represented as lattice sites that were fixed in a particular spin-orientation. It was shown that these defects had a significant effect on the temperature range of the phase transition, and resulted in a higher average critical temperature . This result is likely due to the defects acting as nucleation sites and, thereby, decreasing the energetic barrier to magnetisation.

Computational Modelling Group

Introducting Defects into the Ising Model

Categories