Can the principle of Maximum Entropy Production be used to predict the steady states of a Rayleigh-Bernard convective system?

Investigators: Kevin Oliver, Iain Weaver, James Dyke

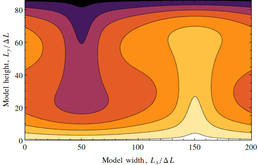
Convection cell configurations produced by the modified lattice Boltzmann model. Contours show isotherms and are shaded light to dark with decreasing temperature.

The principle of Maximum Entropy Production (MEP) has been successfully used to reproduce the steady states of a range of non-equilibrium systems. Here we investigate MEP and maximum heat flux extremum principles directly via the simulation of a Rayleigh-Bérnard convective system implemented as a lattice gas model. Heat flux and entropy production emerges in this system via the resolution of particle interactions. In the spirit of other related works, we use a reductionist approach, creating a lattice-Boltzmann model to produce steady-convective states between reservoirs of different temperatures. Convection cells emerge that show meta-stability where a given lattice size is able to support a range of convective states. Slow expansion and contraction of the model lattice, implemented by addition and subtraction of vertices, shows hysteresis loops where stable convection cells are expanded to regions wherein they become meta-stable, and eventually transition into more stable configurations. The maximally stable state is found to be that which maximises the rate of heat transfer, which is only equivalent to maximum internal entropy production in a strong forcing regime, while it is consistent with minimising entropy production in a weak forcing case. These results demonstrate the utility of lattice-Boltzmann models for future studies of non-equilibrium systems, and highlight the importance of dissipation and forcing rates in disambiguating proposed extremum principles.

Computational Modelling Group

Can the principle of Maximum Entropy Production be used to predict the steady states of a Rayleigh-Bernard convective system?

Categories