Vibrational spectroscopy from ab initio molecular dynamics

Started: 3rd June 2013
Ended: 20th September 2013
Research Team: Valerio Vitale
Investigators: Hans Fangohr, Chris-Kriton Skylaris

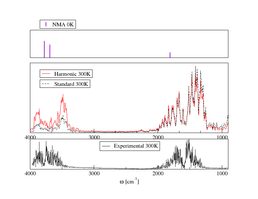
Computed (red) and experimental (black) spectra of water. The former have been obtained by applying the Fourier transform to the dipole moment autocorrelation function.

In this project I used the Fourier transform of the time correlation function (FTTCF) formalism, that allows to compute the vibrational spectra of molecules both in gas and condensed phase, at finite temperature, in a single ab initio molecular dynamics simulation. Ab initio molecular dynamics simulations means that the dynamics of the system under inspections is (partially) described in terms of quantum mechanical (QM) equations. In particular, we adopted Born-Oppenheimer molecular dynamics-BOMD, which allows to treat electrons and their interactions through QM and the motion of nuclei classically. We implement our code within the ONETEP [1] program, a linear-scaling density functional theory based code.

The central idea is to calculate the dipole moment of the system at each time step, even if this can be a tricky task for a quantum system when periodic boundary conditions are applied. Then at the end of the simulation we have a time series of the dipole moments. We calculate the autocorrelation function of this time series and then the Fourier transform of the autocorrelation. We have to use quantum correction factors as we are treating nuclei classically. This approximation, brings to a symmetry breaking that must be restored with these quantum correction factors, see figure.

For the integration of the equations of motion, we use the following scheme: at each time step the electronic orbitals are evaluated by minimising the total energy of the system with nuclei fixed at their previous positions, through a selfconsistent DFT scheme. Once that the electronic configuration has been evaluated, the positions and momenta of nuclei are updated using the velocity-Verlet integrator. Consequently, at the next time step nuclei are in a new configuration that in turn gives a new electronic configuration and therefore new forces on nuclei. If the time step is sufficiently small, i.e. approximatively 0.5 femtoseconds, the total energy is conserved and no long term drifts appear.

[1] C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, J. Chem. Phys. 122, 084119 (2005)

Computational Modelling Group

Vibrational spectroscopy from ab initio molecular dynamics

Categories