Efficient algorithms for liquid crystal alignment
- Homepage
- http://www.personal.soton.ac.uk/dales/DFQTA/
- Investigators
- Giampaolo D'Alessandro, Timothy Sluckin
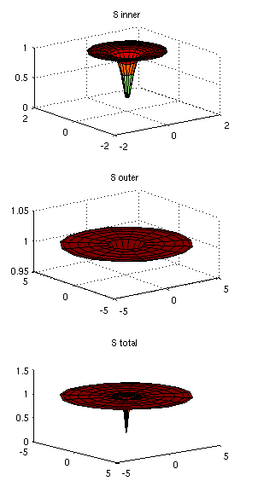
Simulation of a defect in liquid crystals - Core (top), approximate outer layer (middle) and merging of the two (bottom).
Liquid crystals are best known for their applications in modern flat screens, but other technologically important applications include colour-sensitive thermometers, temperature-sensitive paints, optoelectronic equipment such as shutters and sensors, materials such as ultra-light body armour, as well as very recently in microfluidic devices-on-a-chip. They are also materials of great fundamental interest because they exhibit some liquid-like properties (they flow) and some solid-like properties (their properties depend on direction). Despite intense theoretical work over the last forty years, it is still the case that new applications require a more fundamental mathematical understanding of liquid crystalline models in order that rapid device prediction can be made.
A major headache in liquid crystal theory is the so-called "defect" problem. Liquid crystals usually exhibit a preferred direction, but this preferred direction can change from place to place. The defects are lines or points near which the preferred direction dissolves. An analogy can be seen when one combs one's hair: it is impossible to comb hair uniformly over a sphere; there will always be some holes in the pattern. Cosmologists have also use the liquid crystal defects as models of the early universe. The internal patterns of the defects also provide the dramatic and beautiful characteristic optical signatures for individual types of liquid crystal.
Describing them has caused much difficulty in mathematical theories of liquid crystals. The standard theory (due to the Scottish mathematician Frank Leslie) just omits them, while alternative approaches ("the Q-tensor" theory) often are computationally inefficient in regions in which the preferred direction changes only slowly. In the latter case, even when there is a computational model for the liquid crystal properties, it may be difficult to provide a physical picture. The end result is that properties of new devices cannot be predicted reliably and quickly.
Our project will provide a more sophisticated model of the motion of defected nematic liquid crystals. We shall build on anew mathematical approximation which we have recently developed. This approach, which we have labelled the Defect- free Q-tensor approximation (DFQTA), uses the best features of the Leslie and Q-tensor approaches. In non-defected liquid crystals, this approach has led to dramatic improvements (of the order of a factor of 100) in the computational time required to solve some benchmark problems, without any loss of accuracy. Our new model will treat defect motion by patching together solutions in the defect-free and defected regions. The defect-free region will be treated using DFQTA. The defect itself will be cut out of the problem, and treated separately using a range of approximations made possible by the fact, amongst others, that the regions that contains them are small. The two regions will be matched using asymptotic analysis. Our approach will combine the algorithmic requirements of engineers (who often downplay the necessity for mathematical analysis), with sophisticated mathematical approximation tools to obtain an accurate and computationally efficient model.
Categories
Physical Systems and Engineering simulation: Complex fluids, Electromagnetism, Liquid crystals, Photonics