Magnetic dynamics under the Landau-Lifshitz-Baryakhtar equation

Research Team: Weiwei Wang
Investigators: Hans Fangohr

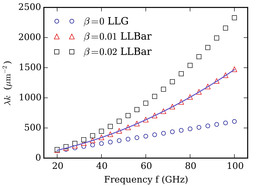
A comparison between LLG and LLBar for the spin wave decay.

The fundamental Landau-Lifshitz-Gilbert (LLG) equation has been broadly used in Micromagnetics to govern the magnetization dynamics. The key term in the LLG equation is the Gilbert damping which is a phenomenal scalar constant that has the relativistic origin and is local. Despite the fact that the local damping failed to explain some experimental data as well as in contradiction microscopic calculation, the nonlocal damping was indeed observed, such as the enhanced damping in thin ferromagnetic films due to the spin pumping to the adjacent nonmagnetic conducting layers. Interestingly, the intrinsic nonlocal damping is also observed recently. In this project, we implemented the Landau-Lifshitz-Baryakhtar (LLBar) equation in a finite element Micromagnetic package. Baryakhtar developed a new equation for magnetic moment using Onsager’s kinetic equations, in the exchange approxmation there is an exchange damping which actually describe the nonlocal damping. We study the spin wave decay, domain wall motion and the linewidth of magnonic resonances using the implemented micromagnetic package.

Computational Modelling Group

Magnetic dynamics under the Landau-Lifshitz-Baryakhtar equation

Categories