Measuring organisation with statistical complexity
- Started
- 1st October 2012
- Ended
- 1st June 2013
- Research Team
- David Arden
- Investigators
- Seth Bullock
What is pattern, structure, or organisation? How can we measure it? Can we automate the process of picking out the spontaneous emergence of patterns from noise? Is it even possible to say with any reasonable certainty that the organisation of a dynamic system is increasing or decreasing?
Probably not, but we'll give it a go anyway.
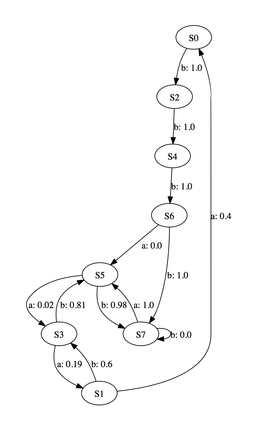
From the field of computational mechanics, we have a measure of the organisation of a system, called statistical complexity. This is a measure based on how hard it is to predict the future of a system, given previous observations.
By making a large number of observations of a system, we can use an algorithm called Causal State Splitting Reconstruction (CSSR) to pick out any repeated patterns or structure in the system just by their statistical similarites. From these repeated patterns we can construct an abstract representation of the underlying dynamics of the system, called an epsilon-machine (which is somewhat similar to a finite-state automata).
The epsilon-machine is the unique minimal, optimal predictor of a system. Hence it is reasonable to say that the complexity (the information entropy) of the epsilon-machine is the (statistical) complexity of the system, and that an increase in statistical complexity indicates an increase in organisation (pattern, structure or whatever).
However, what happens when we actually put data from a system that is becoming more organised over time into CSSR? If the changes are happening too fast, the algorithm might not have time to collect sufficient data to perform the required statistical analysis.
If CSSR is to be a useful tool in investigating the spontaneous emergence of patterns from noise, we need to better understand how it responds to such data. It may be possible to calibrate the algorithm to compensate, or to adapt the algorithm in some other way. It may be that the difficulties in using CSSR can inspire us to develop a better approach to investigating (self-)organising systems.
Categories
Algorithms and computational methods: statistical analysis
Programming languages and libraries: Python
Transdisciplinary tags: Complex Systems