Hadronic structure on the computer

Research Team: Dirk Broemmel, Thomas Rae, Ben Samways
Investigators: Jonathan Flynn

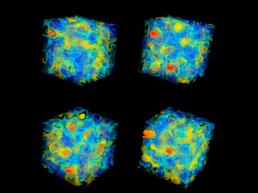
Topological charge: illustrating one aspect of one of our 4D gauge field configurations as a 3D slice (RBC/UKQCD collaboration)

Our best description of the strong force - a fundamental force describing the interactions between partons (quarks and gluons) that make up hadrons (e.g. protons and neutrons) - is Quantum Chromo-Dynamics (QCD). QCD exhibits two defining properties: confinement (which means that quarks cannot be isolated and are forever bound in hadrons) and asymptotic freedom (which means that in high energy reactions the quarks and gluons interact weakly). These phenomena can both be thought of in terms of the size of the coupling (which describes the strength of the interactions). In the asymptotically free regime the coupling is small, whereas for confinement, it becomes increasingly large. The most precise measurements to date in QCD have been made using perturbation theory, which involves an expansion in the coupling constant. This is well justified for high energy QCD where the coupling is small. This, however, fails when the coupling constant is large; where the higher order corrections become larger than lower order terms in the perturbative series. This is the case for the low energy regime of QCD where hadronisation occurs and hence we require a non-perturbative theory.

Parton distribution amplitudes (PDAs), structure functions and form factors are non-perturbative hadronic parameters that are required in many QCD calculations. PDAs describe the momentum-fraction distribution of quarks and anti-quarks in hadrons. They can be linked to high energy form factors or the wave function of the meson (bound state of a quark and anti-quark). Experimental input for the PDAs is very limited, as they always appear as part of a convolution and cannot be cleanly isolated in collider experiments and, therefore, theoretical calculations are required. We calculate the lowest (mathematical) moments of the PDAs for several light mesons non-perturbatively on the lattice. Together with our results from the non-perturbative renormalisation (NPR) project, this provides a clear description from first principles that can be compared to, and used for, experiment.

Lattice QCD simulations allow for a first-principle non-perturbative calculation of quantum mechanical matrix elements, using Monte Carlo evaluation of functional integrals with enormous numbers of variables. Ensembles of field configurations distributed according to the action of the quantum field theory are generated using a Markov process, and are subsequently used to calculate correlation functions from which matrix elements can be extracted. Both steps in the calculation require inversions of large sparse matrices. The physics has local interactions and thus the simulations are well-suited for massively parallel computers. Each processor deals with a chunk of the lattice, with halo exchange between processors for field values on the boundaries of the chunks and occasional global sums over the entire lattice. In our project, we use Iridis to calculate correlation functions from which we can isolate the moments of parton distribution amplitudes.

The calculations are performed within the UKQCD and RBC collaborations.

Computational Modelling Group

Hadronic structure on the computer

Categories