Renormalisation group approach to 1D cellular automata with large updating neighbourhoods

Investigators: Iain Weaver, Adam Prugel-Bennett

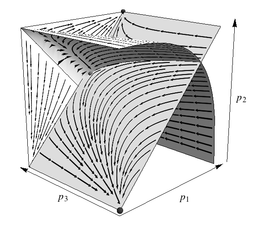
The intersection of the Domany-Kinzel and CDP planes with the critical plane. Renormalisation flow in the critical plane is towards the fixed point of the renormalisation group. The plane therefore describes a set of PCA which share identical large-scale

We study self-similarity in one-dimensional probabilistic cellular automata (PCA) by applying a real-space renormalisation technique to PCA with increasingly large updating neighbourhoods. By studying the flow about the critical point of the renormalisation, we may produce estimates of the spatial scaling properties of critical PCA. We find that agreement between our estimates and experimental values are improved by resolving correlations between larger blocks of spins, although this is not sufficient to converge to experimental values. However applying the technique to PCA with larger neighbourhoods, and therefore more renormalisation parameters, results in further improvement. Our most refined estimate produces a spatial scaling exponent, found at the critical point of the five-neighbour PCA, of nu=1.056 which should be compared to the experimental value of nu=1.097.

Computational Modelling Group

Renormalisation group approach to 1D cellular automata with large updating neighbourhoods

Categories