A Mathematical Analysis of the Driving Force of Perivascular Drainage in the Brain

Started: 10th June 2013
Ended: 20th September 2013
Research Team: Alexandra Diem
Investigators: Giles Richardson, Roxana-Octavia Carare

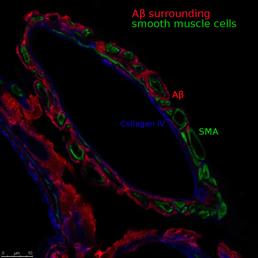
Image of a cerebral artery during AD. A? is colocalised with the components of the basement membrane, suggesting that these are the drainage pathways of perivascular drainage.

The observation that perivascular drainage in the brain occurs in the reverse direction of the blood flow has for a long time been puzzling for researchers. While arterial pulsations have been suggested as the driving force for the drainage of soluble proteins such as A?, it did not explain the directionality of the flow. Our model implements a simple valve mechanism that can explain the reverse flow of ISF, which is based on realistic structural assumptions. The findings have potential implications for AD research in the search for preventive medication.

Alzheimer's Disease (AD) is the most common form of dementia and although it has been researched for over 100 years to date there is no treatment. Its onset and progression is closely related to the accumulation of the neuronal metabolite A?, which raises the question of how metabolites are eliminated from the brain normally. In recent years a connection between the pathology of AD and cerebrovascular diseases has been discovered. Interstitial fluid (ISF), which flows in the basement membranes (BM) of cerebral arteries have been found to be the pathways for perivascular drainage with arterial pulsations as the pumping mechanism. However, perivascular drainage appears to occur in the reverse direction of the blood flow, which cannot be explained solely by arterial pulsations. In this study a mathematical model of perivascular drainage using a flap-like valve mechanism is introduced, which only allows for unidirectional flow. The results of this model suggest that such a valve can promote net reverse flow in the perivascular spaces (PVS) and that this valve may be realised by conformational changes of the BM proteins.

Our model of ISF flow through the BM is based on Darcy's Law using a nonlinear permeability function to describe a valve mechanism. The BM is very narrow (100 nm) and therefore it is reasonable to assume thin film flow, which, together with the continuity equation, forms the governing equations of the model. The flow is driven by a travelling wave on the boundary of the ISF and artery, which models the heart-rate driven pulsation of arteries.

Using this model it can be shown analytically that a net reverse flow in the PVS cannot be achieved without a valve. Therefore the implementation of a valve mechanism via conformational changes of the BM proteins is justified. The use of the valve mechanism leads to a net reverse drainage in the PVS and therefore our model provides a possible explanation of the reverse solute drainage in the brain, which is based on realistic assumptions.

Computational Modelling Group

A Mathematical Analysis of the Driving Force of Perivascular Drainage in the Brain

Categories