The Maximum Entropy Production Principle and Natural Convection

Research Team: Stuart Bartlett
Investigators: Seth Bullock, James Dyke

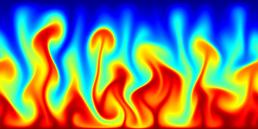
A turbulent convection flow in which a fluid is heated from below and cooled from above. Colour corresponds to temperature. This simulation is in an initial transient phase in which thermal plumes are growing and 'competing'.

Natural convection occurs in fluids which exhibit flow due to differential heating. The flow is caused by the fact that heating a fluid parcel reduces its density and density gradients induce a net flow since heavier fluid will tend to displace lighter fluid if the latter is located below the former. A common configuration for experiments on natural convection consists of a closed container which is heated from below and cooled from above. Heat is transported through the system by a combination of conduction at the boundaries and convection flow in the interior (see image).

In principle this experimental setup can be implemented in two different ways. The first consists of forcing a fixed quantity of heat into the system per unit time at the lower boundary, and extracting an equal amount of heat from the upper boundary. This is a constant flux boundary condition and forces the temperature gradient at the system boundaries (proportional to heat flux due to Fourier's law of conduction) to remain at a constant value. Alternatively one can fix the boundary temperatures, instead of the boundary heat fluxes. In this case the amount of heat that enters or leaves the system can be of arbitrary value, the only constraint is that the boundary temperatures remain constant. Fixed temperature boundaries can also be described as infinitely conducting since there is no limit on the boundary temperature gradient (the internal heat flux is limited by the finite thermal conductivity and the finite rate of convective transport of the fluid).

We can then ask, under these two different boundary conditions, are there any macroscopic variables which the system maximises or minimises? This question is relevant because experiments with different fluid properties have shown that the bulk heat flux increases as the viscosity of the fluid decreases (lower viscosity allows a greater degree of convective heat transport). This is true in the constant boundary temperature system but in the constant flux system the bulk flux is fixed by the boundary conditions. In this case it turns out that as the viscosity decreases, the average net temperature difference across the system decreases. So is there a macroscopic variable which is being optimised in both cases?

There are several key variables describing the system: total heat flux, total temperature gradient and entropy production. With fixed flux boundary conditions, we prescribe the heat flux, and the temperature gradient and entropy production can vary. With fixed temperature boundaries, the temperature gradient is prescribed, and the flux and entropy production vary. It has been shown that convecting systems in fact maximise heat flux under the constraint of fixed boundary temperatures (as well as hydrodynamic constraints) [Malkus, 1954]. Since entropy production is the product of heat flux with the difference between the two inverse temperatures, it also increases with heat flux and temperature gradient. So for the fixed temperature system, it seems that entropy production is maximised. What about the fixed flux system? In this case the temperature gradient actually decreases as the fluid becomes better able to transport heat. So here it seems that entropy production is actually being minimised.

In addition to the two boundary conditions I have described, there are a range of other ways we could induce temperature gradients in the system. One set of conditions, sometimes called negative feedback boundary conditions, involves applying constant inward fluxes of heat at the boundaries, and then allowing outward heat fluxes which are linearly proportional to the boundary temperature (see schematic diagram in the image gallery on the profile page). For this system neither the total temperature difference or the heat flux is held constant, the magnitudes of these variables emerges from the relative balance of the fluxes and internal hydrodynamic properties. What is interesting about such boundary conditions is that the entropy production, instead of monotonically increasing or decreasing with one of the key variables, actually exhibits a peak at intermediate values of total temperature difference. Could this maximum represent some kind of non-equilibrium attractor for such systems? Some authors have found that in highly turbulent systems such as planetary atmospheres, this is indeed the case [Ozawa, 2003]. What about the slightly simpler case of a single phase fluid? I have been investigating this question using Lattice Boltzmann simulations. I have written a code which takes advantage of the local nature of the Lattice Boltzmann method. It uses MPI routines to allow complete parallelisation and I have been running simulations on the Iridis 4 supercomputer. Without the use of several hundred, high power processors like those of Iridis 4, simulating the more turbulent flows would simply be impossible.

The results of my simulations have shown that in fact simple convective fluids do not tend to this peak in entropy production. In fact they adhere to the same scaling of dimensionless variables seen in the constant flux and constant temperature cases. We can understand this result by remembering that there is no reason for the negative feedback boundary conditions to fundamentally alter the force-flux behaviour inherent to natural convection. The fluid system is driven out of equilibrium and responds by trying to return to equilibrium. The boundary conditions, combined with the physical properties of the fluid, determine the rate of heat transport possible and so there is no reason that different fluids should all settle to the same heat flux (corresponding to maximum entropy production). If we were dealing with heat flow by diffusion the system's macroscopic equations could be solved exactly because a diffusive system responds linearly to imposed driving forces. The only additional feature unique to the convective system is that it responds non-linearly to imposed driving forces. However it still responds in a consistent manner (e.g. decreasing viscosity increases heat flux). I believe that any imposed boundary conditions would cause the same scaling between dimensionless variables as long as they cannot diverge (this would be the case if for example, the inward heat flux was made proportional to boundary temperature, then the temperature would soon tend to infinity).

However maximum entropy production does seem to apply to the transport of heat by atmospheric circulation. Therefore, this leaves open the question of what extra degrees of freedom are required before the entropy maximisation seen in atmospheric heat transport occurs in these simpler systems.

The first phase of this work has now been published in the journal Physical Review E: http://journals.aps.org/pre/abstract/10.1103/PhysRevE.90.023014

Computational Modelling Group

The Maximum Entropy Production Principle and Natural Convection

Categories