Stuart J. Bartlett
- Position
- Postgraduate Research Student
- Institution
- Electronics and Computer Science (FPAS)
- Contact
- Complete this online contact form to contact Stuart.
Broadly speaking, I'm interested in the transition from non-living to living. We currently have only one observable system in which this transition has taken place, which makes it a particularly challenging problem.
The study of this one (special?) case attempts to re-construct the geochemical state of the early Earth and deduce the steps, which life may have taken from complex chemistry to simple single-celled organisms endowed with some form of genome. The evolution of life on Earth from that point on is slightly more straightforward to piece together with the use of phylogenetic analyses.
Rather than contribute to this effort, I have chosen to ask a more general question which is strongly linked to the definition of life: What is required for a system to become living?
One attempt at defining life has been through the idea of autopoiesis of Maturana and Varela. This theory states that an enclosed, defined unit is living if it is separated from its environment by some form of semi-permeable boundary (the boundary cannot be closed since material and/or energy must pass through it to sustain the living unit), and within that boundary is contained a set of structures and interactions which act to maintain the existence of those structures and the enclosing boundary. Hence an autopoietic system functions as both the means and the end for its own persistence. It operates such that it can continue or expand its operations.
Clearly there are some problems with this definition for life. Far enough away from the context of an organism's environment, it cannot survive, and all known living organisms do not persist indefinitely. Therefore it could be argued that a flame is living since one could define a boundary separating the flame from its surroundings and claim that within the flame are a set of processes which allow it to persist. The set of processes are much simpler than those of a contemporary organism but autopoiesis makes no mention of some threshold degree of internal complexity. If the flame runs out of fuel or oxygen, it soon ceases to exist as an organism would if deprived of the basic flows of nutrients or free energy it crucially requires.
This raises the interesting issue of non-living structures or patterns which show some life like characteristics. Reaction diffusion spots are a primary example of such systems. These are distinct spatial patterns in which the rate at which 'reactant' molecules diffuse inwardly is balanced by the rate at which they react and form a 'product' which diffuses outwardly. When such systems are embedded within a bath of reactant they will persist indefinitely and can also be observed to expand and divide such that a primitive replication occurs. These systems can exhibit a myriad array of patterns such as spiral waves and stripes. When further reactions and chemical species are added the complexity of the patterns increases concomitantly.
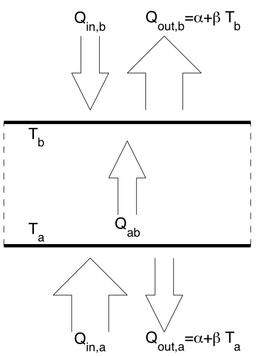
Certain fluid dynamical structures also show some resistance to perturbations and primitive adaptation. Examples are convection cells in heated fluid systems and hurricanes. These are further examples of what are collectively known as 'dissipative structures', a term usually attributed to the chemist Ilya Prigogine. Dissipative structures are formed in systems which are driven away from equilibrium because of free energy gradients (e.g. gradients of temperature or chemical potential). Some dissipative structures are simple such as the round cells in laminar natural convection and others are more complex (organisms can be viewed as dissipative structures since they rely on free energy gradients for their maintenance and reproduction).
A further interesting property of dissipative structures is that while they appear to be internally organised, this organisation allows them to produce a significant quantity of entropy. Although entropy is only rigorously defined for isolated systems, it is intuitively associated with the degree of disorder in a system (or equivalently, the degree of ignorance that an observer has over the state of a system). What are the driving forces which control the degree to which these systems become organised? Is their formation a manifestation of the systems attempts to equilibrate as rapidly as possible? What limits or augments the complexity of these structures? If a dissipative structure becomes sufficiently complex could it be described as living? Is there a continuum of patterns between simple dissipative structures and organisms? Was the transition to life on Earth a process of dissipative structures becoming more complex as they gained the ability to respond to their environments, encode information and gain some degree of autonomy not exhibited by simpler dissipatve structures?
These are some of the questions which guide my research. I intend to investigate the thermodynamic properties of systems, which form dissipative structures, essentially to test the extent of the analogy between dissipative structures and biological structures. I will be simulating pattern-forming, non-equilibrium systems with an increasing number of degrees of freedom. Starting with thermally driven fluids, I will then add passive solute species and define a thermodynamically consistent set of reactions between them. As I add more and more chemical species into the reaction network, I will observe how the morphology of the structures changes as a function of the number of species/reactions increases and also measure the entropy production to see whether additional degrees of freedom allows the system to dissipate free energy at a higher rate and if so how this increase scales with degrees of freedom.
Working with...
 Seth Bullock Seth BullockProfessor, Electronics and Computer Science (FPAS) |
Research Groups
Institute for Complex Systems Simulations (ICSS)
University of Southampton
Science and Engineering of Natural Systems group
Electronics and Computer Science (FPAS)
Projects
Cellular Automata Modelling of Membrane Formation and Protocell Evolution
With Seth Bullock (Investigator)

The Maximum Entropy Production Principle and Natural Convection
With Seth Bullock, James Dyke (Investigators)
Gallery
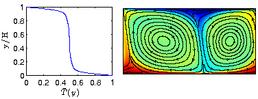
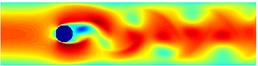
Natural convection in a single phase fluid. On the left is the mean temperature as a function of vertical coordinate. On the right is the temperature field.
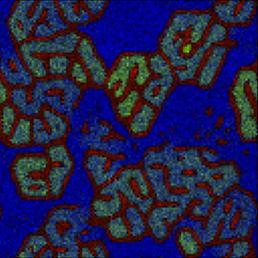
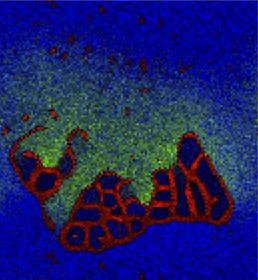
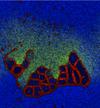
Reproduction of Ono's (2001) results on the spontaneous emergence of cell-like structures in a simple lattice artificial chemistry.
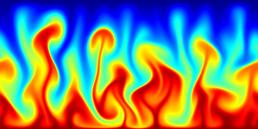
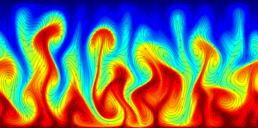
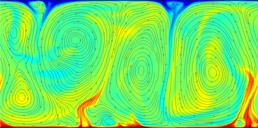
A turbulent convection flow in which a fluid is heated from below and cooled from above. Colour corresponds to temperature. This simulation is in an initial transient phase in which thermal plumes are growing and 'competing'.