A novel approach to analysing fixed points in complex systems

Research Team: Iain Weaver
Investigators: James Dyke

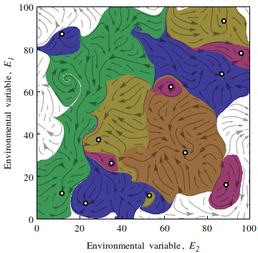
Distinct, complex attractors form (coloured regions) shown here for a two-dimensional environment. The time evolution of the system is along streamlines, towards fixed points (open circles).

Complex systems are frequently characterised as systems of many components whose interactions drive a plethora of emergent phenomena. Understanding the history and future behaviour of planet Earth, arguably the most complex known system in the universe, is an ambitious goal and remains at the core of complexity science. From the establishment of the planet's magnetic dipole, to the interplay between life and it's environment. The dynamics across all scales are characterised by their numerous interacting components.

Of particular interest is how such a system may be stable at all, and the role of life in establishing this apparent stability. The model demonstrates that even random couplings between many many species, and a multidimensional environment can produce stable, and robust configurations. The model is found to be invariant with the number of biotic components past a lower limit. Additionally, rather than increases in environmental complexity leading to a reduction in the possibility of steady states, it is proven that the converse is true, suggesting that the proposed mechanism may be applicable to even high dimensional complexity.

The extent to which this observation is general, rather than being unique to the intricacies of the model may only be revealed by thorough analysis. Rather than enumerating the effects of individual species, we show that such a system can be described as a Gaussian process, which enables novel analytical, and efficient computational techniques to be employed.

Iain S. Weaver and James G. Dyke, 2013, A novel approach to analysing fixed points in complex systems, Proceedings of the European Conference on Complex Systems 2012, ch65

Computational Modelling Group

A novel approach to analysing fixed points in complex systems

Categories