A Fast Multipole Method for the Bessel potential
- Started
- 9th December 2009
- Research Team
- Neil O'Brien
- Investigators
- Marc Molinari, Simon Cox
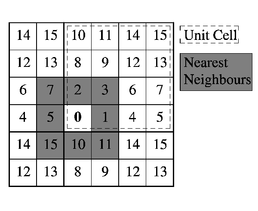
The unit cell is divided into child cells and we calculate the effect of particles within a child (here, no. 0) on well-separated child cells (shown in white) via a multipole coefficient rather than using expensive direct computation.
The fast multipole method (FMM) proposed by Greengard and Rokhlin provides a method by which the O(N-squared) many-body problem can be reduced to O(N) complexity. In this project, a multipole method is developed to calculate the energy of a system of vortices in a high temperature superconductor, where the many-body interactions give rise to rich and complex physics. The method developed here is suitable for systems where the interactions are governed by a Bessel potential rather than the usual logarithmic potentials occurring in gravitational and electrostatic problems. We derive and apply vectorised forms of the Gegenbauer addition formulae in order to achieve the O(N) scaling associated with fast multipole methods.
Categories
Physical Systems and Engineering simulation: Superconductivity
Algorithms and computational methods: Multipole methods
Visualisation and data handling software: Gnuplot
Software Engineering Tools: SVN
Programming languages and libraries: C, Fortran, GPU-libs, Matlab