Precision study of critical slowing down in lattice simulations of the CP^{N-1} model

Started: 2nd June 2014
Research Team: Andrew Lawson
Investigators: Jonathan Flynn, Andreas Juttner

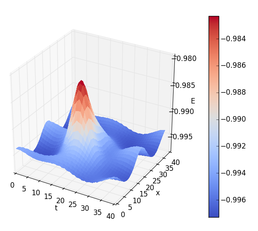
Energy distribution across the lattice for an example field configuration after smoothing out quantum fluctuations. The red peak indicates the presence of a non-trivial topological structure.

The Markov chain Monte Carlo algorithm that is employed in lattice QCD simulations requires the generation of a sequence of 4-dimensional lattices, each populated with a unique configuration quantum fields. The Monte Carlo algorithm itself is responsible for evolving the system from one field configuration into another. However multiple hits of the Monte Carlo update procedure are required to produce a new configuration that is fully decorrelated from the previous one. This notion of correlation will also vary depending upon exactly what type of measurement we wish to extract from our configurations. For observables related to topology, one typically requires a larger number of Monte Carlo updates required to produce a new statistically independent configuration.

The phenomenon of critical slowing down (CSD) arises when we make the spacing of our discrete lattice finer, i.e. when we move closer to the continuum theory. For particular observables this decrease in lattice spacing leads to an increase in the number of Monte Carlo update steps that are required to produce an independent configuration; this increase in Monte Carlo 'relaxation time' is referred to as CSD. For topological observables the number of update steps appears to increase exponentially as the lattice is made finer. In order to study this algorithmic property it is useful to perform numerical experiments. As QCD simulations are extremely expensive, we instead study these algorithms using the 2-dimensional CP^{N- 1} model. This model exhibits similar properties to QCD, such as confinement, and has non-trivial topology. Crucially however, it is much less costly to simulate and thus provides a much more convenient framework in which to test algorithmic developments.

In this project we used the Iridis cluster to carry out extensive numerical simulations of the CP^{N-1} model in order to study the phenomenon of CSD. We performed a series of simulations, each with a different lattice spacing in order to test the scaling of CSD as we move closer to the continuum theory. We developed a highly- optimised Monte Carlo algorithm such that each simulation of a particular lattice spacing would take advantage of all cores of a single compute node and make efficient use of the vectorisation capabilities of the CPUs. Each simulation was carried out with a sufficiently long Monte Carlo history in order to accurately quantify the characteristics of the CSD; by utilising Iridis we were able to run all our simulations concurrently such that they completed within a few weeks. As a result we accurately quantified the nature of CSD for key observables within the model. Future aims for this project involve modifying the boundary conditions used in the simulation, which may allow for a faster rate of decorrelation of the field configurations for the purpose of measuring topological quantities.

Computational Modelling Group

Precision study of critical slowing down in lattice simulations of the CP^{N-1} model

Categories