Diffusion
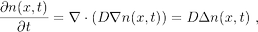
Diffusion is a wide-spread phenomenon with prime examples being the diffusive behaviour of, say, salt or some chemical substance, in a liquid, or the spread of heat through a sample.

(Animation has been taken from http://en.wikipedia.org/wiki/File:Heat_eqn.gif)
For queries about this topic, contact Hans Fangohr.
View the calendar of events relating to this topic.
Projects

Centre for Doctoral Training in Next Generation Computational Modelling
Hans Fangohr, Ian Hawke, Peter Horak (Investigators), Susanne Ufermann Fangohr, Thorsten Wittemeier, Kieran Selvon, Alvaro Perez-Diaz, David Lusher, Ashley Setter, Emanuele Zappia, Hossam Ragheb, Ryan Pepper, Stephen Gow, Jan Kamenik, Paul Chambers, Robert Entwistle, Rory Brown, Joshua Greenhalgh, James Harrison, Jonathon Waters, Ioannis Begleris, Craig Rafter
The £10million Centre for Doctoral Training was launched in November 2013 and is jointly funded by EPSRC, the University of Southampton, and its partners.
The NGCM brings together world-class simulation modelling research activities from across the University of Southampton and hosts a 4-year doctoral training programme that is the first of its kind in the UK.

Diffusion at solute/solvent interfaces
Anatoliy Vorobev (Investigator), Ruilin Xie
We aim to develop the theoretical model that would provide an accurate description for the mixing process of two miscible liquids, and, in particular, would reproduce our experimental optical observations. The model based on the phase-field (Cahn-Hilliard) approach is adopted for the mixture of two miscible liquids. The model takes into account the surface tension effects, the non-Fickian diffusion across the liquid/liquid interface, and hydrodynamic flows that might be generated near the interface by the concentration gradients.

Investigation into the Interfacial Physics of Field Effect Biosensors
Nicolas Green, Chris-Kriton Skylaris (Investigators), Benjamin Lowe
This interdisciplinary research aims to improve understanding of Field Effect Transistor Biosensors (Bio-FETs) and to work towards a multiscale model which can be used to better understand and predict device response.

Multiscale Modelling of Cellular Calcium Signalling
Hans Fangohr, Jonathan Essex (Investigators), Dan Mason
Calcium ions play a vitally important role in signal transduction and are key to many cellular processes including muscle contraction and cell apoptosis (cell death). This importance has made calcium an active area in biomedical science and mathematical modelling.

Porous Media and Hydrothermal Circulation in Weakened Ocean Crust
Formation of oceanic crust is an interplay between magma and the cooling hydrothermal system above that its own heat drives. To understand this system we must understand where and how water circulates through the crust.
Ocean crust is riddled with faults and other permeable pathways along which water preferentially flows. We seek to use basic numerical models of circulation in porous media to understand how much of an influence on crust formation these anomalous features have, compared to the bulk, unfractured crust.
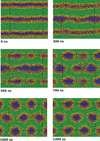
Simulation of biological systems at long length and distance scales
Jonathan Essex (Investigator), Kieran Selvon
This project aims to shed light on cell membrane mechanisms which are difficult to probe experimentally, in particular drug permiation across the cell membrane. If one had a full understanding of the mechanism, drugs could be designed to target particular embedded proteins to improve their efficacy, the viability of nano based medicines and materials could also be assessed, testing for toxicity etc.

The Ca-geospeedometer - A tool for investigating the processes that generate oceanic crust
We quantify the errors inherent in the current methods of geospeedometry, which lets one obtain the cooling rate of a rock, using mineral trace element chemistry. Calcium-in-Olivine geospeedometry is useful for deep ocean crust.
We want to use this proxy to figure out how ocean crust actually accretes, it provides key evidence as to how magma chambers and hydrothermal systems interact to produce new lithosphere. But to do so we first have to determine how reliable the method is and therefore how much can be inferred from results.

The Maximum Entropy Production Principle and Natural Convection
Seth Bullock, James Dyke (Investigators), Stuart Bartlett
In this project I wanted to perform some tests of the so-called Maximum Entropy Production Principle (MEPP) in the context of buoyancy-driven convection in a system with negative feedback boundary conditions.

Using MEP to determine parameter values of ocean and atmosphere diffusivity
Kevin Oliver, James Dyke (Investigators), Maike Sonnewald
Entropy budgets can potentially offer new and valuable insights into the dissipation of energy in the ocean system. Specifically, if one assumes the Earth system maximises the dissipation of energy, one can use this as a guiding principle maximising the internal entropy production. In this study, resultant temperature distributions from a four box ocean-atmosphere-ice model are used to assess to what extent such considerations could ameliorate the need for tuning parameter values associated with oceanic and atmospheric diffusivity. Results from a standard implementation with fixed, empirically determined, parameters were compared to one where the maximum entropy production principle is applied to determine the value of oceanic and atmospheric diffusivity parameters. These methods have been successfully applied to cloud fraction and convection in the atmosphere.
The MEP principle suggested using diffusivity values of 3.3×1014 W K ?1 and 3.2×1014 W K ?1
for the ocean and atmosphere respectively, where the empirical values were 2.0 × 1014 W K ?1
and 1.0 × 1014 W K ?1 . The oceanic temperatures of the MEP implementation were 3 and -1oC
away the high and low latitude observed ocean temperatures respectively, while the empirical
implementation was -5 and 3oC away, largely within the observational standard deviation of
8 and 2? C respectively. For the atmospheric values, MEP implementation was 3W m?2 away
from the high latitude observed value, while the empirical implementation was 6W m?2 away,
both within the standard deviation of 13.2W m?2 . However, in the low latitudes this reverses,
with the empirical implementation being only -16W m?2 off while the MEP implementation
is -21W m?2 off. However, both figures are outside the range of the standard deviation of
4.2W m?2 . Overall, both methods were found to be very close to oceanic observations. This
confirms that in the model used, the assumption of maximal dissipation of energy is reasonable.
Furthermore, the nature of the landscape of internal entropy production created by the
oceanic and atmospheric diffusivity was found to be fairly smooth, with non-linearities mainly
coming from ice albedo. Assuming the Earth system is in a state of maximal energy dissipa-
tion, applying the MEP principle successfully may depend on such a smooth, easily optimisable
landscape. Thus, the successful application of the MEP principle could be much more difficult
if attempting to aid parametrisation in more detailed ocean models, as these are likely to have
internal entropy production landscapes with local maxima. Nevertheless, results presented
are very promising, and encourage further exploration of to what extent this principle could
be applied to ameliorate the need for tuning parameters in light of lacking information.
People
 Seth Bullock
Seth BullockProfessor, Electronics and Computer Science (FPAS)
 Jonathan Essex
Jonathan EssexProfessor, Chemistry (FNES)
 Hans Fangohr
Hans FangohrProfessor, Engineering Sciences (FEE)
 Nicolas Green
Nicolas GreenReader, Electronics and Computer Science (FPAS)
 Peter Horak
Peter HorakReader, Optoelectronics Research Centre
 James Dyke
James DykeLecturer, Electronics and Computer Science (FPAS)
 Ian Hawke
Ian HawkeLecturer, Mathematics (FSHS)
 Kevin Oliver
Kevin OliverLecturer, National Oceanography Centre (FNES)
 Chris-Kriton Skylaris
Chris-Kriton SkylarisLecturer, Chemistry (FNES)
 Anatoliy Vorobev
Anatoliy VorobevLecturer, Engineering Sciences (FEE)
 Stuart Bartlett
Stuart BartlettPostgraduate Research Student, Electronics and Computer Science (FPAS)
 Ioannis Begleris
Ioannis BeglerisPostgraduate Research Student, Engineering Sciences (FEE)
 Rory Brown
Rory BrownPostgraduate Research Student, Civil Engineering & the Environment (FEE)
 Jamie Caldwell
Jamie CaldwellPostgraduate Research Student, Engineering Sciences (FEE)
 Paul Chambers
Paul ChambersPostgraduate Research Student, Engineering Sciences (FEE)
 Robert Entwistle
Robert EntwistlePostgraduate Research Student, Engineering Sciences (FEE)
 Stephen Gow
Stephen GowPostgraduate Research Student, Engineering Sciences (FEE)
 Joshua Greenhalgh
Joshua GreenhalghPostgraduate Research Student, Engineering Sciences (FEE)
 James Harrison
James HarrisonPostgraduate Research Student, Engineering Sciences (FEE)
 Nicholas Hill
Nicholas HillPostgraduate Research Student, Electronics and Computer Science (FPAS)
 Benjamin Lowe
Benjamin LowePostgraduate Research Student, Electronics and Computer Science (FPAS)
 David Lusher
David LusherPostgraduate Research Student, Engineering Sciences (FEE)
 Juraj Mihalik
Juraj MihalikPostgraduate Research Student, Engineering Sciences (FEE)
 Alvaro Perez-Diaz
Alvaro Perez-DiazPostgraduate Research Student, Engineering Sciences (FEE)
 Daniel Powell
Daniel PowellPostgraduate Research Student, Engineering Sciences (FEE)
 Craig Rafter
Craig RafterPostgraduate Research Student, Engineering Sciences (FEE)
 Hossam Ragheb
Hossam RaghebPostgraduate Research Student, Engineering Sciences (FEE)
 Sabin Roman
Sabin RomanPostgraduate Research Student, University of Southampton
 Kieran Selvon
Kieran SelvonPostgraduate Research Student, Engineering Sciences (FEE)
 Ashley Setter
Ashley SetterPostgraduate Research Student, Engineering Sciences (FEE)
 Maike Sonnewald
Maike SonnewaldPostgraduate Research Student, National Oceanography Centre (FNES)
 Jonathon Waters
Jonathon WatersPostgraduate Research Student, Engineering Sciences (FEE)
 Thorsten Wittemeier
Thorsten WittemeierPostgraduate Research Student, Engineering Sciences (FEE)
 Martin Wood
Martin WoodPostgraduate Research Student, Ocean & Earth Science (FNES)
 Ruilin Xie
Ruilin XiePostgraduate Research Student, Engineering Sciences (FEE)
 Emanuele Zappia
Emanuele ZappiaPostgraduate Research Student, Engineering Sciences (FEE)
 Susanne Ufermann Fangohr
Susanne Ufermann FangohrAdministrative Staff, Civil Engineering & the Environment (FEE)
 Jan Kamenik
Jan KamenikAlumnus, University of Southampton
 Dan Mason
Dan MasonAlumnus, University of Southampton