Computational Modelling Group

A novel approach to analysing fixed points in complex systems

James Dyke (Investigator), Iain Weaver

This work aims to contribute to our understanding of the relationship between complexity and stability. By describing an abstract coupled life-environment model, we are able to employ novel analytical, and computational techniques to shed light on the properties of such a system.

Ab initio simulations of chemical reactions on platinum nanoparticles

Chris-Kriton Skylaris (Investigator), Álvaro Ruiz-Serrano, Peter Cherry

•Use first principles calculations to study the relationship between shape and size of nanoparticle and the oxygen adsorption energy.

• Investigate the effect of high oxygen coverage on the catalytic activity of the nanoparticles.

Can the principle of Maximum Entropy Production be used to predict the steady states of a Rayleigh-Bernard convective system?

Kevin Oliver, Iain Weaver, James Dyke (Investigators)

The principle of Maximum Entropy Production (MEP) has been successfully used to reproduce the steady states of a range of non-equilibrium systems. Here we investigate MEP and maximum heat flux extremum principles directly via the simulation of a Rayleigh-Bérnard convective system implemented as a lattice gas model.

Centre for Doctoral Training in Next Generation Computational Modelling

Hans Fangohr, Ian Hawke, Peter Horak (Investigators), Susanne Ufermann Fangohr, Thorsten Wittemeier, Kieran Selvon, Alvaro Perez-Diaz, David Lusher, Ashley Setter, Emanuele Zappia, Hossam Ragheb, Ryan Pepper, Stephen Gow, Jan Kamenik, Paul Chambers, Robert Entwistle, Rory Brown, Joshua Greenhalgh, James Harrison, Jonathon Waters, Ioannis Begleris, Craig Rafter

The £10million Centre for Doctoral Training was launched in November 2013 and is jointly funded by EPSRC, the University of Southampton, and its partners.

The NGCM brings together world-class simulation modelling research activities from across the University of Southampton and hosts a 4-year doctoral training programme that is the first of its kind in the UK.

Fidelity optimisation in an atomic quantum computer

Timothy Freegarde (Investigator), Jack Saywell

Development of optimised composite pulses for atomic quantum computers with the aim of reducing systematic errors in information processing caused by variations in laser intensity and environment.

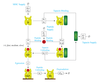
Immunotherapy Research: Modelling MHC Class I Complex Assembly

Timothy Elliott, Jorn Werner (Investigators), Alistair Bailey

This project uses mathematical modelling and simulation to investigate mechanisms by which our cells process and present biological information that is used by our immune system to distinguish between healthy and diseased cells.

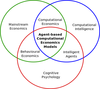
It takes all sorts: the mathematics of people’s behaviour in financial markets

Valerio Restocchi (Investigator), Frank McGroarty, Enrico Gerding

Agent-based models provide a deeper understanding of financial markets than classic models. We model people's behaviour and use agent-based simulations to study financial markets. By analysing the emerging complex dynamics, we achieve a deeper understanding of market participants' behaviours, which are necessary for a deeper comprehension of financial markets themselves.

Microstructural modeling of skin mechanics

Georges Limbert (Investigator), Emanuele Zappia

Microstructural modeling of skin mechanics to gain a mechanistic insight into the biomechanics of the skin.

Modelling the Combined Effects of Total Ionizing Dose and Random Dopant Fluctuations in sub-100 nm gate-length Transistors

Kees de Groot (Investigator), Eleni Chatzikyriakou

The radiation hardness of state-of-the-art silicon-on-insulator transistors of gate length dimensions of 90 nm and beyond is investigated. The combined effects of oxide charges and random fluctuations of the dopant atoms in silicon are considered. It is demonstrated that a parasitic channel forms at the interface of buried oxide and shallow trench isolation regions of the device and that this effect is aggravated by random dopant fluctuations.

Nonlinear Optics in Structured Material

Peter Horak, Neil Broderick (Investigators)

Structured materials such as photonic crystals, optical fibres, Bragg gratings etc. are the ideal material for nonlinear optics. Properly engineered materials allows one to control which nonlinear interactions are observed and enhanced whilst other nonlinear interactions can be neglected. This work looks both at fundamental ideas as well as the fabrication of devices for advanced telecommunications.

Pushing the Envelope of Planetary Formation and Evolution Simulations

Peter Bartram

A full understanding of the formation and the early evolution of the Solar System and extrasolar planetary systems ranks among natural science's grand challenges, and at present, even the dominant processes responsible for generating the observed planetary architecture remain elusive.

Renormalisation group approach to 1D cellular automata with large updating neighbourhoods

Iain Weaver, Adam Prugel-Bennett (Investigators)

We study self-similarity in one-dimensional probabilistic cellular automata (PCA) by applying a real-space renormalisation technique to PCA with increasingly large updating neighbourhoods. By studying the flow about the critical point of the renormalisation, we may produce estimates of the spatial scaling properties of critical PCA.

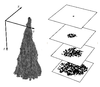
Renormalisation of 2D cellular automata with an absorbing state

Adam Prugel-Bennett, Iain Weaver (Investigators)

We describe a real-space renormalisation scheme for non-equilibrium probablistic cellular automata (PCA) models, and apply it to a two-dimensional binary PCA. An exact renormalisation scheme is rare, and therefore we provide a method for computing the stationary probability distribution of states for such models with which to weight the renormalisation, effectively minimising the error in the scale transformation.

Self-Force and Black Hole Inspirals

Sam Dolan (Investigator)

We use IRIDIS to compute the self-force acting on a solar-mass black hole orbiting a supermassive black hole.

The importance of timescales for the emergence of environmental self-regulation

Iain Weaver, James Dyke (Investigators)

Models which explore the possibilities of emergent self-regulation in the Earth system often assume the timescales associated with changes in various sub-systems to be predetermined. We analyse a classic model of environmental self-regulation, Daisyworld, and interpret the original equations for model temperature, changes in insolation, and self-organisation of the biota as an important separation of timescales.

Tipping points in Complex Coupled Life-Environment Systems

Iain Weaver, James Dyke (Investigators)

System-level homeostasis has been demonstrated in a number of conceptual, artificial life, models which share the advantage of a thorough and transparent analysis. We reintroduce a general model for a coupled life-environment model, concentrating on a minimal set of assumptions, and explore the consequences of interaction between simple life elements and their shared, multidimensional environment.

Using MEP to determine parameter values of ocean and atmosphere diffusivity

Kevin Oliver, James Dyke (Investigators), Maike Sonnewald

Entropy budgets can potentially offer new and valuable insights into the dissipation of energy in the ocean system. Specifically, if one assumes the Earth system maximises the dissipation of energy, one can use this as a guiding principle maximising the internal entropy production. In this study, resultant temperature distributions from a four box ocean-atmosphere-ice model are used to assess to what extent such considerations could ameliorate the need for tuning parameter values associated with oceanic and atmospheric diffusivity. Results from a standard implementation with fixed, empirically determined, parameters were compared to one where the maximum entropy production principle is applied to determine the value of oceanic and atmospheric diffusivity parameters. These methods have been successfully applied to cloud fraction and convection in the atmosphere.

The MEP principle suggested using diffusivity values of 3.3×1014 W K ?1 and 3.2×1014 W K ?1
for the ocean and atmosphere respectively, where the empirical values were 2.0 × 1014 W K ?1
and 1.0 × 1014 W K ?1 . The oceanic temperatures of the MEP implementation were 3 and -1oC
away the high and low latitude observed ocean temperatures respectively, while the empirical
implementation was -5 and 3oC away, largely within the observational standard deviation of
8 and 2? C respectively. For the atmospheric values, MEP implementation was 3W m?2 away
from the high latitude observed value, while the empirical implementation was 6W m?2 away,
both within the standard deviation of 13.2W m?2 . However, in the low latitudes this reverses,
with the empirical implementation being only -16W m?2 off while the MEP implementation
is -21W m?2 off. However, both figures are outside the range of the standard deviation of
4.2W m?2 . Overall, both methods were found to be very close to oceanic observations. This
confirms that in the model used, the assumption of maximal dissipation of energy is reasonable.

Furthermore, the nature of the landscape of internal entropy production created by the
oceanic and atmospheric diffusivity was found to be fairly smooth, with non-linearities mainly
coming from ice albedo. Assuming the Earth system is in a state of maximal energy dissipa-
tion, applying the MEP principle successfully may depend on such a smooth, easily optimisable
landscape. Thus, the successful application of the MEP principle could be much more difficult
if attempting to aid parametrisation in more detailed ocean models, as these are likely to have
internal entropy production landscapes with local maxima. Nevertheless, results presented
are very promising, and encourage further exploration of to what extent this principle could
be applied to ameliorate the need for tuning parameters in light of lacking information.